In the two previous posts, I have written about functional conditions both in individuals and in groups. In the previous part 2, I described, among other things, the Havana syndrome, where much suggests that it was not an attack from a foreign power but instead a psychogenic condition that spread within social networks. In this section, I intend to delve deeper into what social networks generally look like and what facilitates the spread of new ideas. First, I will go through basic graph theory, and then a bit more about a new article that has leveraged social contagion to spread an intervention in a poor area.
It started in Königsberg
One can use networks or graphs as an abstraction of different relationships. Suppose you want to describe a social network where you represent each person as a node and each relationship as an edge. The degree of a node is the number of friends that a person has. The distance between two nodes is then the number of edges one needs to pass through. Clusters are also mentioned, where one measures how many of a node's neighbors are also neighbors with each other. All of these properties affect how information spreads in the network and how robust they are against different nodes being knocked out. The Swiss mathematician Leonhard Euler was early interested in graphs, as exemplified in the problem of how to best navigate around the city of Königsberg (now Kaliningrad) with its seven bridges. The city is situated on two islands, and the problem was to navigate around by only crossing each bridge once. Euler developed graph theoretical concepts and showed that this problem has no solution!
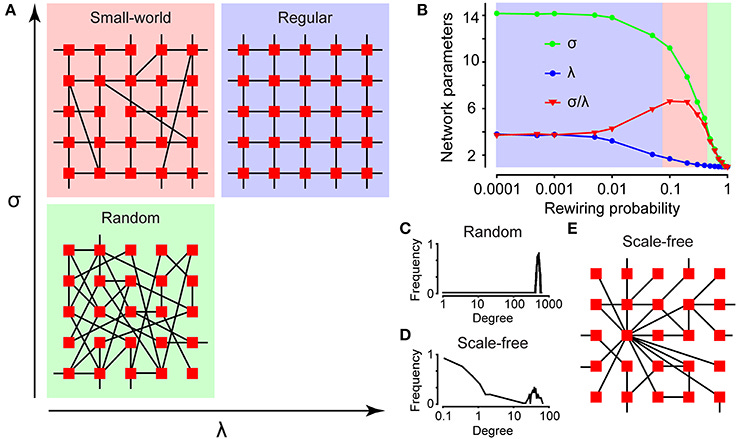
Networks were something I was interested in as a doctoral student when I studied immature neurons during development and how they communicate with each other. By measuring the activity in each cell and then pairwise comparing how similar they were between cells, one can build up a functional network. Then I used graph theoretical methods to characterize the constructed networks. We showed that immature neurons form networks with two overarching properties: small-worldness and scale-freeness (read more here).

That a network is scale-free means that there is no typical scale for how many neighbors a particular node has (see C compared to D in the figure below). If one were to plot the distribution of the number of neighbors, it would have a tail towards some nodes having disproportionately many neighbors (especially in a logarithmic scale as in C and D below). These are also called hubs.
The model for how scale-free networks are formed was developed by Barabási and Albert (read here). In short, it's about when a network grows, it's not evenly distributed how new nodes connect to the existing ones. By letting the probability be proportional to the number of existing neighbors, those with many neighbors get even more. This is sometimes called rich get richer. In a scale-free network, hubs are of significant importance as they connect many different parts of a network. An example could be an influencer in social media or a major airport in the world's network of flight connections. Such a network is also robust against random nodes being knocked out.
Regarding small-world networks, it's about them having both average short paths between nodes and high clustering density (low lambda and high sigma in the figure above to the left, the red quadrant). Watts and Strogatz showed what properties these networks have and how they can be created. An example is also social networks where it turns out that the average distance between two people in the world is shorter than one might think. Your friend's friend knows someone who is friends with Bill Gates.
The Friendship Paradox
If you ask people how many friends they have and how many friends their friends have, it turns out on average that friends have more friends than they do. This turned out to be a mathematical property of networks that can be perceived as counterintuitive (see article here). An advantage of such social networks is that you can more efficiently reach larger groups. Say you want to convey certain information and want to reach as many people as possible, or rather enough people. There are different ways to do this:
One secure but expensive way is to contact everyone.
Another way is to randomly reach a certain percentage of the group.
A third way is to reach out to hubs.
The problem with number three is that one rarely knows which ones are hubs. A clever alternative is then to ask a random percentage of people about their friends instead. This is something exploited in a very recent study in Science. There, they wanted to test how to best deliver an educational intervention to poor communities in Honduras. They reasoned that by using this method, they would maximize social contagion and thus achieve better dissemination of the educational intervention. Since they worked with a large number of remotely located villages, they could randomize how they contacted people: either randomly or through friends. Then they examined a number of outcomes to see if a certain intervention reached more people with one method or the other. The authors summarize it as:
We find that a meaningful improvement in maternal and child health outcomes can be achieved by deploying friendship-nomination targeting with an educational intervention of the kind that is typical of public health and development economics practice. This effect manifests a threshold, however, which in turn varies by outcome, which means that different fractions of seeds needed to be used for different outcomes of interest, depending on how hard the outcome is to modify in the first place or depending on whether a change in knowledge, attitudes, or practices is the objective.
Conclusion
In this post, I have described how social networks can be seen as avenues to disseminate both information and psychogenic contagions. If a certain portion of a social network begins to believe in something or perceives themselves affected by something, this can spread to friends. At the end of the previous post, I reasoned about various culture-bound syndromes and how they can spread. A relatively recent example is various forms of motor tics, especially among young people, which have increased in the USA and England. This can be seen as a culture-bound syndrome or even a functionally neurological symptom that has spread, particularly in connection with the COVID-19 pandemic when many were isolated at home (read more here). There are examples of individuals with a significant social media reach exhibiting motor tics, which then spread to other young people. More research is needed here on how to identify such conditions and how to respond to individuals affected by the condition in a respectful yet evidence-based manner.